
Fórmula de Bhaskara: Para que serve e como usar?

No complexo mundo da matemática, existem inúmeras fórmulas e cálculos que os alunos usam para resolver diversos problemas. A fórmula de Bhaskara é uma das mais estudadas e temidas pelos alunos. Esse artigo que o Colégio Amplo preparou para você, vai te mostrar para que serve e como usar essa fórmula que já tirou o sono de muita gente. Confira!
Fórmula de Bhaskara
Essa fórmula nada mais é do que um método para encontrar as raízes reais de uma equação do segundo grau fazendo uso apenas de seus coeficientes. Vale lembrar que coeficiente é o número que multiplica uma incógnita em uma equação. Em sua forma original, a fórmula de Bhaskara é dada pela seguinte expressão:
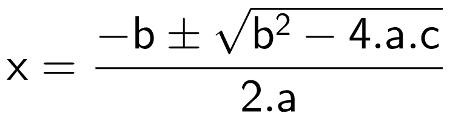
Para utilizar essa fórmula, vale lembrar que toda equação do segundo grau deve ser escrita da seguinte forma:
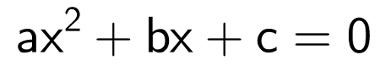
Entendendo a equação
Os coeficientes dessa equação são os números que ocupam o lugar de “a”, de “b” e de “c”. Portanto, o coeficiente “a” é o número que multiplica x2; o coeficiente “b” é o número que multiplica x; e o coeficiente “c” é o número que não multiplica incógnita.
Como aplicar a fórmula de Bhaskara para resolver as equações?
Resolver uma equação do segundo grau é encontrar os valores de x ou da incógnita do problema que fazem com que essa equação seja igual a zero.
A fórmula de Bhaskara apenas exige que o valor numérico de cada coeficiente seja substituído. Após isso, basta você realizar as operações matemáticas indicadas pela fórmula para obter as raízes da equação. Mas esse método é dividido em três etapas para facilitar a compreensão dos alunos.
Calcule a discriminante
Discriminante é a expressão presente dentro da raiz na fórmula de Bhaskara. É comumente representado pela letra grega Δ (Delta) e recebe esse nome pelo fato de discriminar os resultados de uma equação da seguinte forma:
Δ < 0, então a equação não possui resultados reais;
Δ = 0, então a equação possui apenas um resultado real ou possui dois resultados iguais.
Δ > 0, então a equação possui dois resultados distintos reais.
Para calcular as raízes de uma equação do segundo grau, primeiramente calcule o valor numérico de Δ.
Substitua a discriminante e os coeficientes na fórmula de Bhaskara
Geralmente a fórmula de Bhaskara é ensinada apenas da seguinte forma:
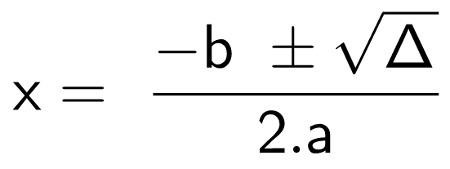
Nessa etapa, basta substituir os valores de Δ e dos coeficientes da equação do segundo grau na fórmula acima.
Calcule as raízes da equação
Você deve ter notado que na fórmula de Bhaskara que existe um sinal “±”. Esse sinal indica que devem ser realizados dois cálculos. O primeiro para o caso em que o número que o segue seja positivo e o segundo para o caso em que o número que o segue seja negativo. É comum nomear cada um desses resultados como x’ e x” ou x1 e x2.
Observe:
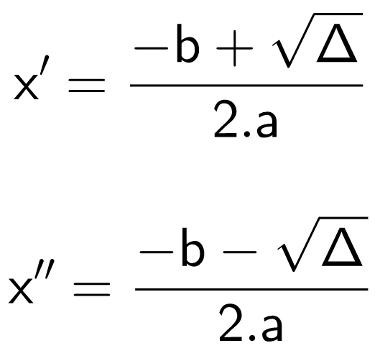
Exemplo:
Calcule as raízes da equação x2 + 12x – 13 = 0.
Utilizando a fórmula de Bhaskara, você deve separar os coeficientes da equação.
a = 1, b = 12 e c = – 13
Δ = b2 – 4ac
Δ = 122 – 4·1·(– 13)
Δ = 144 + 52
Δ = 196
Agora que você tem o valor de Δ, siga adiante:
x = – b ± √Δ
2·a
x = – 12 ± √196
2·1
x = – 12 ± 14
2
Depois, encontre as raízes da equação do segundo grau.
x’ = – 12 + 14
2
x’ = 2
2
x’ = 1
x” = – 12 – 14
2
x” = – 26
2
x” = – 13
Portanto, as raízes da equação x2 + 12x – 13 = 0 são 1 e – 13.




